


The article emphasizes the critical importance of calculating sample size in clinical trials to guarantee reliable and valid results. It provides insights into key statistical parameters and established formulas tailored for various study designs, while addressing common challenges in estimation. An appropriate sample size is not merely a technical requirement; it is essential for ethical research practices and for accurately detecting treatment effects.
In the Medtech landscape, understanding the nuances of sample size calculation is paramount. This knowledge empowers researchers to navigate the complexities of clinical trials effectively, ensuring that their findings are both credible and applicable. Moreover, the article highlights the necessity of collaboration among stakeholders to tackle these challenges head-on.
In conclusion, the significance of calculating sample size cannot be overstated. It is a foundational element that underpins the integrity of clinical research. As researchers and practitioners, taking the necessary steps to address this aspect will enhance the quality and ethical standards of our studies.
Determining the appropriate sample size for clinical trials is a pivotal step that significantly influences the outcomes and credibility of medical research. A well-calculated sample size not only enhances the reliability of results but also ensures that studies are ethically sound and scientifically valid.
However, this process is fraught with challenges, from estimating effect sizes to navigating regulatory requirements. How can researchers effectively balance these complexities to achieve results that truly reflect the efficacy of new treatments? This question lies at the heart of clinical research, urging professionals to consider the implications of their design choices on patient outcomes and the advancement of medical science.
To determine the study's power to detect meaningful differences between treatment groups, it is essential to calculate sample size in a clinical trial. An inadequate number of subjects can make it difficult to calculate sample size clinical trial outcomes, potentially resulting in the dismissal of effective therapies by regulatory bodies, despite their proven advantages.
For instance, a recent trial assessing Drug A's effectiveness in pain reduction required a total of 200 subjects to achieve an 80% power level, accounting for a 10% dropout rate. Conversely, an excessively large cohort can squander resources and unnecessarily expose participants to risks. Striking the right balance is crucial for maintaining both ethical standards and scientific integrity when we calculate sample size clinical trial.
A carefully determined group number is crucial when you calculate sample size clinical trial, as it not only boosts the reliability of the results but also aids informed decision-making in clinical practice. As highlighted in statistical literature, the strength of a test is defined as 1 minus the likelihood of a Type II error, which underscores the necessity to calculate sample size clinical trial to achieve dependable results.
Recent research has demonstrated that in order to calculate sample size clinical trial, larger groups enhance accuracy in effect estimations and tighten confidence intervals, ultimately resulting in more reliable conclusions in clinical investigations.
Furthermore, the extensive clinical trial management services offered by bioaccess—including feasibility studies, compliance evaluations, trial organization, import permits, and efficient project management—play a vital role in establishing the suitable number of participants. By ensuring compliance with regulatory requirements and enhancing the overall quality and reliability of clinical trials, bioaccess contributes to better healthcare outcomes and fosters international collaboration.
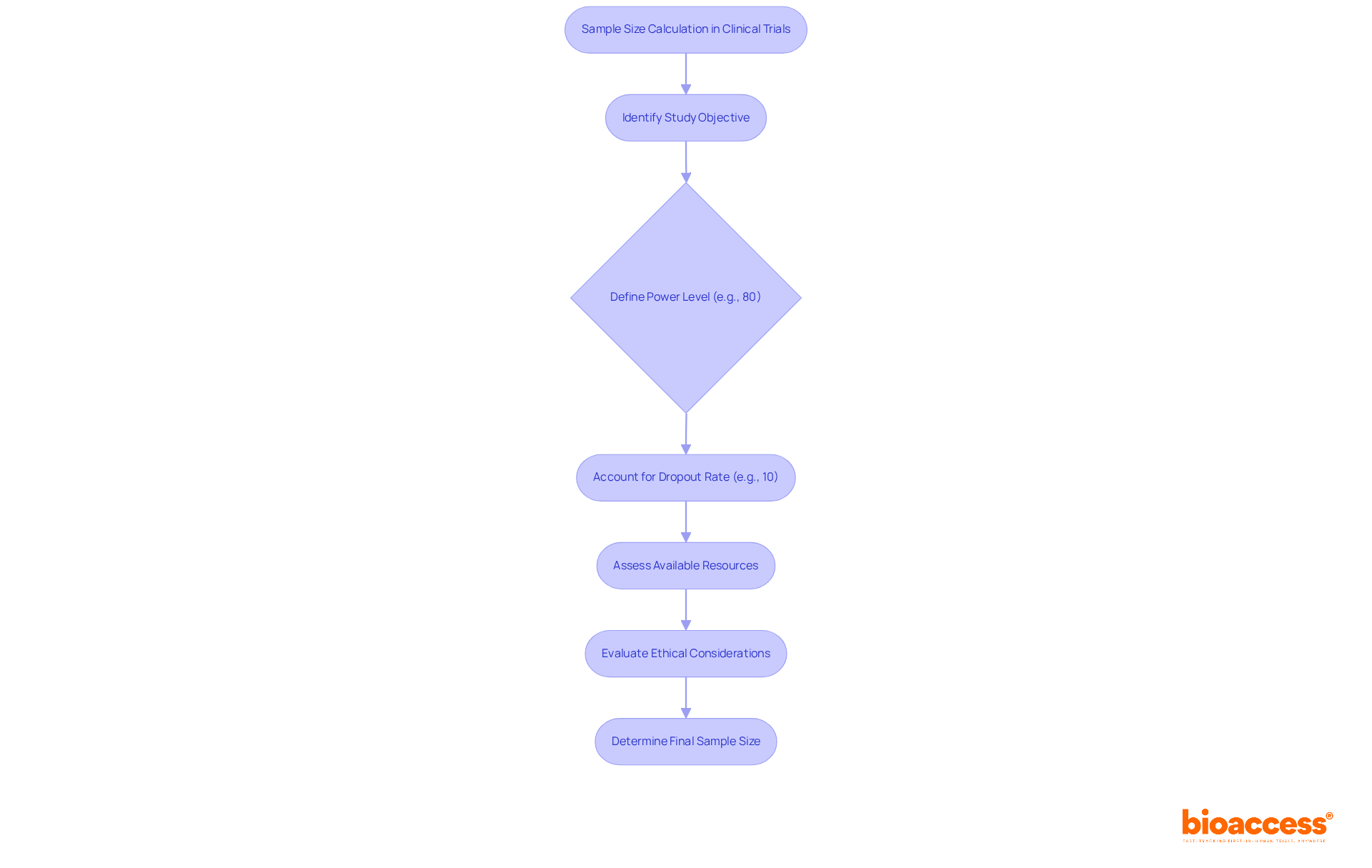
To calculate sample size effectively, it is essential to identify several key statistical parameters:
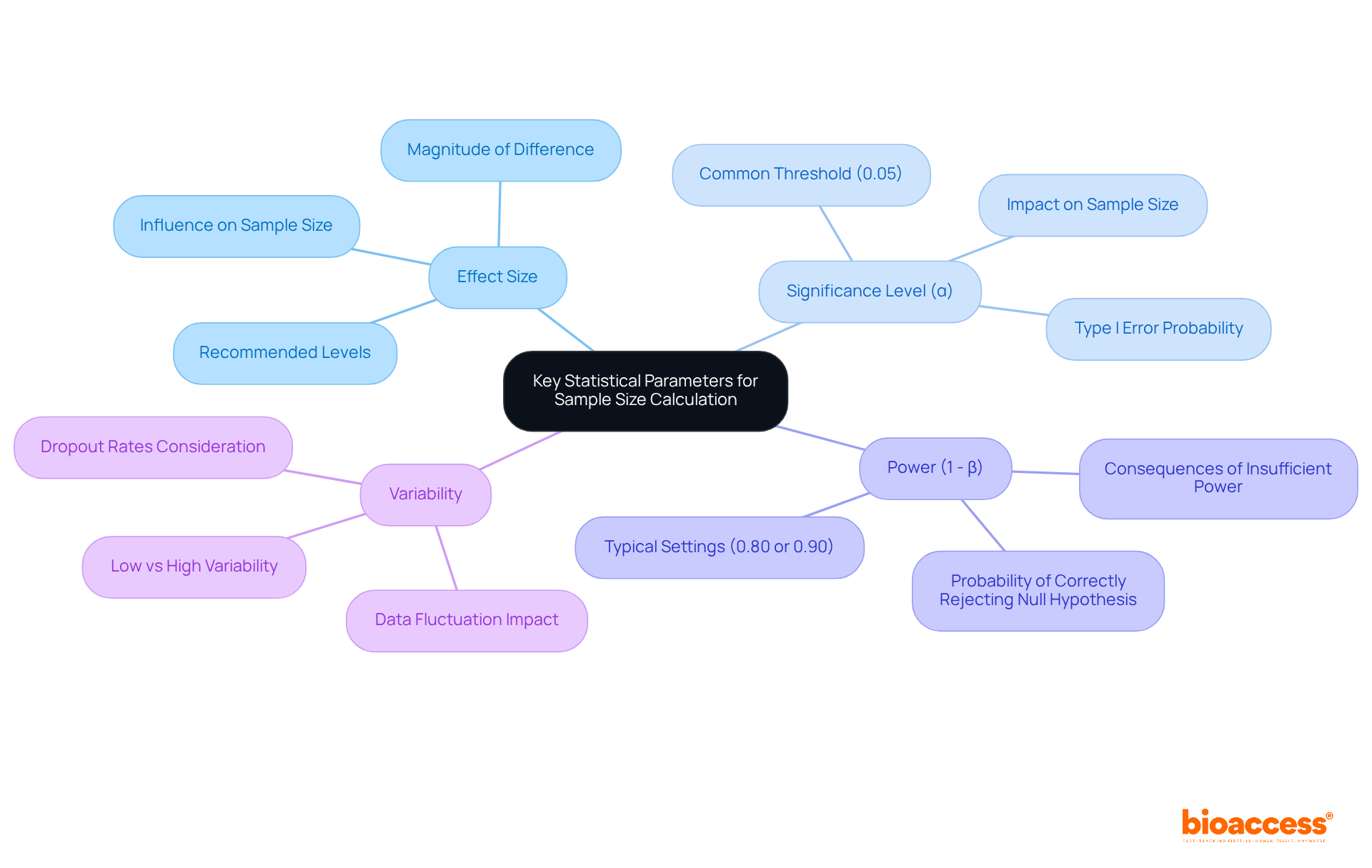
Effect Size: This parameter quantifies the magnitude of the difference expected between groups. A greater magnitude typically enables a smaller group to identify the outcome, making it a crucial factor in trial planning. Research targeting moderate to significant impacts is particularly advised when previous literature is insufficient. As noted by Alaa Althubaiti, researchers should strive for moderate to substantial impact levels when designing research without existing literature.
Significance Level (α): Commonly set at 0.05, this represents the probability of rejecting the null hypothesis when it is true, known as a Type I error. A reduced significance level enhances the rigor of the study but necessitates a greater number of participants to sustain statistical power. The significance level is vital, as it directly influences the probability of identifying genuine outcomes.
Power (1 - β): This is the probability of correctly rejecting the null hypothesis when it is false, often set at 0.80 or 0.90. Increased power indicates a higher probability of identifying genuine outcomes, yet achieving this typically requires a larger sample size. Insufficient power can lead to Type II errors, where genuine outcomes remain unnoticed. Pritha Bhandari emphasizes that ensuring sufficient power is crucial to avoid missing true effects.
Variability: The anticipated fluctuation within the data significantly influences the number of observations. Increased variability necessitates a larger group to attain the same degree of accuracy in results. For instance, research with low variability in results can often operate with fewer participants while still maintaining strong statistical power. Moreover, researchers should factor in potential dropout rates, usually around 10%, to ensure that the final group remains adequate for statistical analysis.
Understanding these parameters is essential, as they directly affect how to calculate sample size for a clinical trial and the overall structure of the studies. Accurately considering effect magnitude, significance threshold, power, and variability guarantees that investigations are sufficiently powered to identify meaningful differences, ultimately enhancing the validity and reliability of research outcomes. Furthermore, neglecting calculations for the number of subjects can lead to the approval of ineffective medications or the dismissal of effective ones, underscoring the ethical implications of this critical step in clinical research.
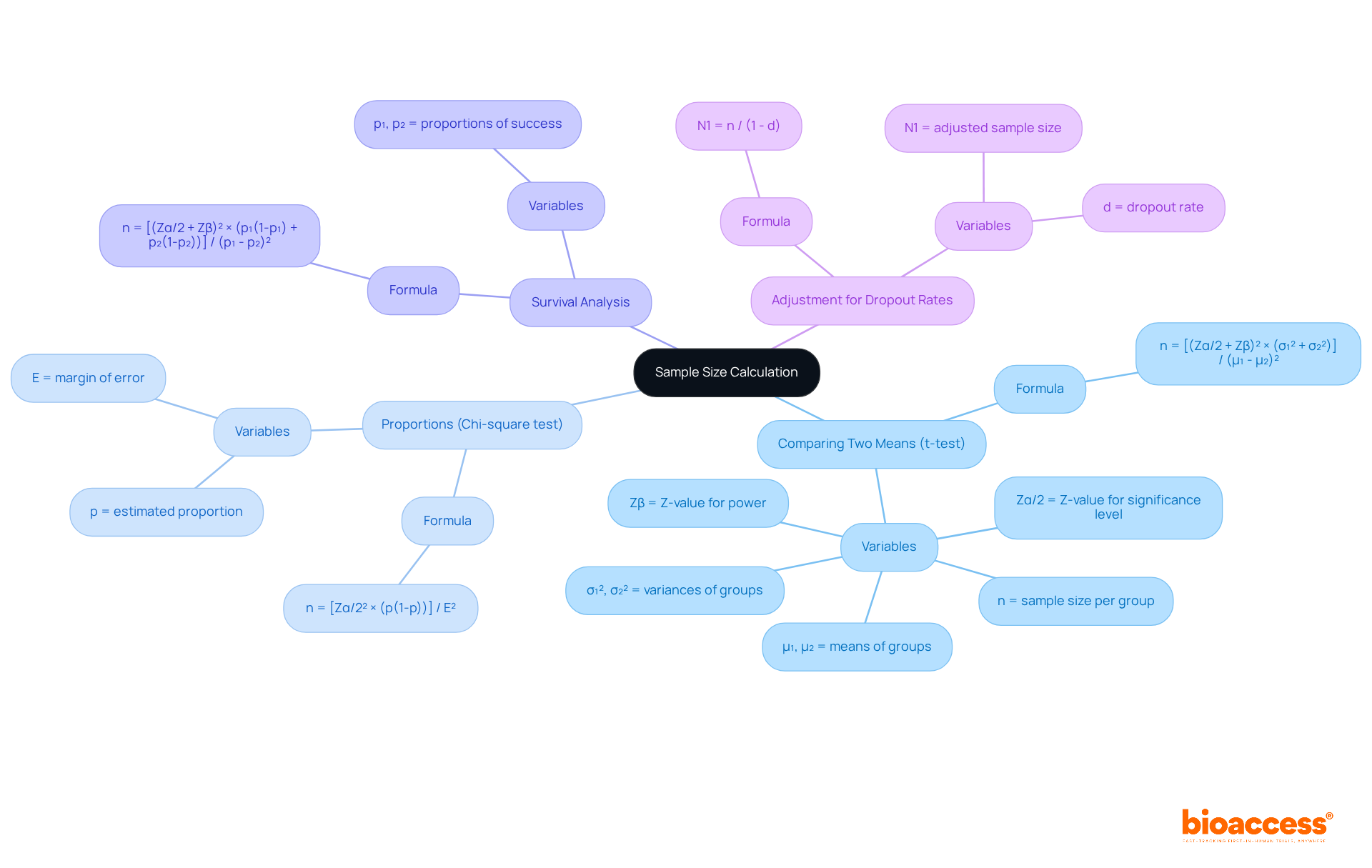
To determine the number of observations in clinical research, it is essential to utilize established formulas tailored to the study design. This section outlines common formulas that are pivotal to calculate sample size clinical trial effectively.
n = [(Zα/2 + Zβ)² × (σ₁² + σ₂²)] / (μ₁ - μ₂)²
Where:
n = [Zα/2² × (p(1-p))] / E²
Where:
n = [(Zα/2 + Zβ)² × (p₁(1-p₁) + p₂(1-p₂))] / (p₁ - p₂)²
Where:
After calculating the initial sample size, it is crucial to adjust for dropout rates using the following formula:
N1 = n / (1 - d)
Where d represents the dropout rate. This adjustment ensures that the final sample quantity accounts for potential participant loss during the study, reinforcing the reliability of the research outcomes.
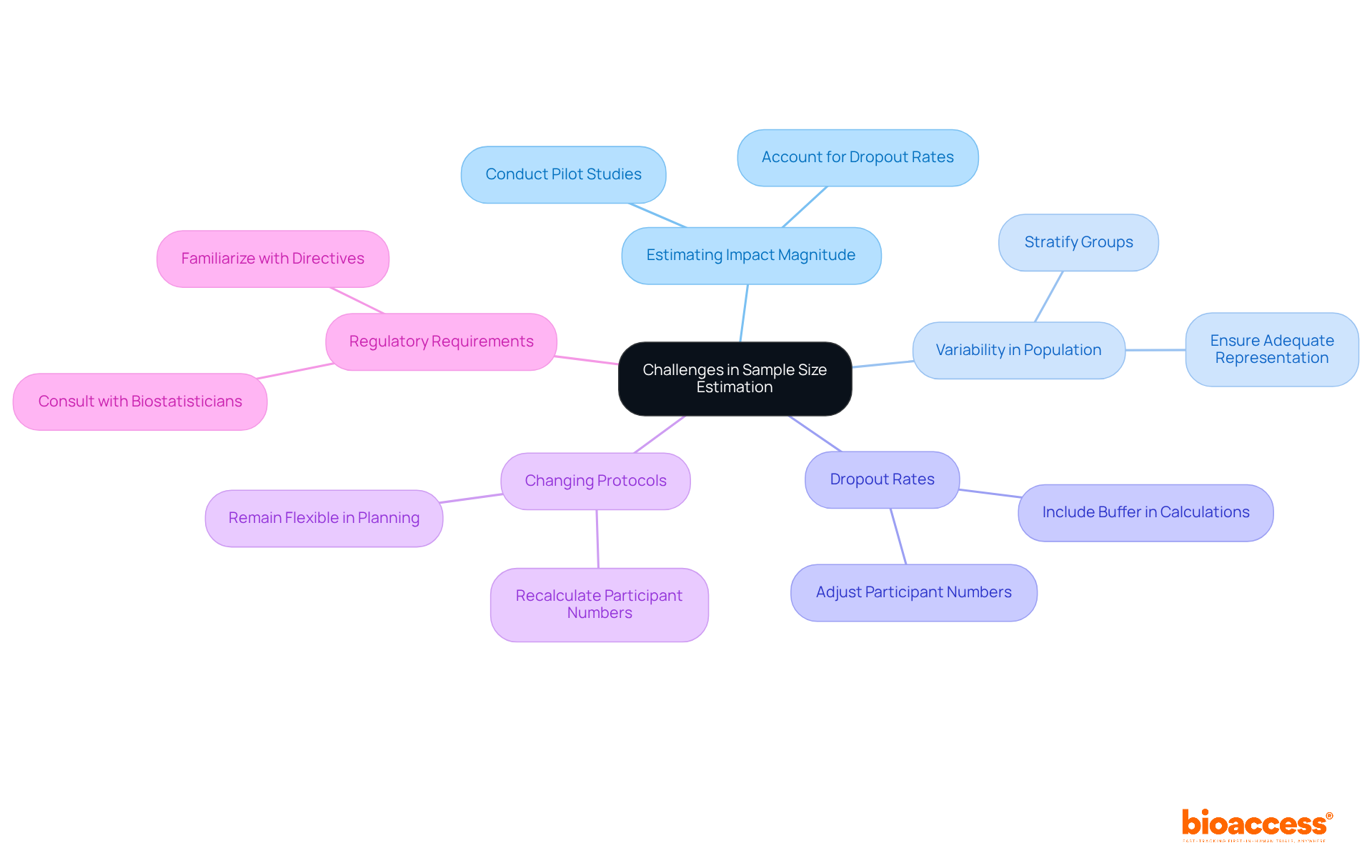
Sample size estimation presents several challenges that researchers must navigate:
Estimating Impact Magnitude: Precisely assessing impact magnitude can be challenging without previous data. Conducting a pilot experiment is a useful approach to collect initial data, significantly improving the precision of effect measurements. For instance, a pilot study may reveal a clinically meaningful difference that informs subsequent calculations. As noted by Tushar Vijay Sakpal, accounting for a dropout rate of 10% indicates that if a cohort of 200 is needed, the modified cohort number should be 220 to preserve statistical power.
Variability in Population: High variability within the target group complicates calculations of the required numbers. To address this, consider stratifying the group to ensure adequate representation across different subgroups, leading to more reliable and generalizable results.
Dropout Rates: Underestimating dropout rates can result in inadequate participant numbers, jeopardizing the research's credibility. It is essential to include a buffer in your calculations to account for potential participant loss. For instance, if a dropout rate of 10% is anticipated, adjust the number of subjects accordingly to maintain statistical power. This modification is crucial, as research often fails to identify significant treatment effects due to insufficient participant numbers.
Changing Protocols: Adjustments to the research framework or endpoints may necessitate recalculating the number of participants. Researchers should remain flexible in their planning to accommodate these changes, ensuring that the study remains adequately powered despite any adjustments.
Regulatory Requirements: Various regulatory authorities may impose specific directives for calculating the number of observations. Familiarizing yourself with these requirements is vital for ensuring compliance and avoiding potential delays in the approval process. Consulting with a biostatistician can provide valuable insights into these guidelines and assist in navigating the complexities of determining the number of observations.
By proactively addressing these challenges, researchers can enhance the robustness of their estimations to calculate sample size clinical trial, ultimately improving the overall quality and reliability of their clinical trials.
Determining the appropriate sample size for clinical trials is a fundamental aspect that significantly influences the outcomes and validity of research. A meticulously calculated sample size not only enhances the reliability of results but also ensures ethical standards are upheld, thereby facilitating informed decision-making in clinical practice. This guide underscores the critical nature of accurately estimating sample sizes to avoid the pitfalls of underpowered studies and the ethical implications of potentially dismissing effective treatments.
Key statistical parameters such as effect size, significance level, power, and variability are essential components in the sample size calculation process. Each parameter plays a pivotal role in shaping the study's design and outcomes, reinforcing the need for precision and careful consideration in planning clinical trials. Challenges such as estimating impact magnitude, addressing variability, and accounting for dropout rates highlight the complexities researchers face in this crucial area.
In conclusion, the significance of proper sample size calculation cannot be overstated. It is imperative for researchers to embrace robust methodologies and remain vigilant in addressing the challenges that arise during the estimation process. By doing so, they contribute to the advancement of clinical research and the development of effective therapies that can ultimately improve patient outcomes. Emphasizing the importance of sample size in clinical trials not only enhances the quality of research but also upholds the ethical standards necessary for the advancement of healthcare.
Why is sample size important in clinical trials?
Sample size is crucial in clinical trials to determine the study's power to detect meaningful differences between treatment groups. An inadequate number of subjects can lead to unreliable outcomes and may result in effective therapies being dismissed by regulatory bodies.
What can happen if the sample size is too small?
If the sample size is too small, it can make it difficult to calculate the outcomes of the clinical trial, potentially leading to the dismissal of therapies that have proven advantages.
What are the consequences of having an excessively large sample size?
An excessively large sample size can waste resources and unnecessarily expose participants to risks, making it important to strike a balance.
How does a well-determined sample size impact clinical trial results?
A carefully determined sample size boosts the reliability of results and aids informed decision-making in clinical practice, enhancing the overall quality of the trial.
What is the significance of the strength of a test in relation to sample size?
The strength of a test, defined as 1 minus the likelihood of a Type II error, underscores the necessity of calculating sample size to achieve dependable results in clinical trials.
How do larger sample sizes affect accuracy in clinical investigations?
Larger sample sizes enhance accuracy in effect estimations and tighten confidence intervals, leading to more reliable conclusions in clinical investigations.
What role does bioaccess play in determining the suitable number of participants for clinical trials?
Bioaccess offers extensive clinical trial management services, including feasibility studies and compliance evaluations, which help establish the appropriate number of participants and ensure regulatory compliance, ultimately improving healthcare outcomes.